Inventing a Better Compression Algorithm for a Specific Problem

Domain-specific knowledge can lead to dramatically better compression results compared to general-purpose algorithms like brotli.

What domain are we entwined with for today?

A game of snake. We are only interested that it can be represented as a sequence of coordinates on infinite (not really) integer space, where the first coordinate is the head of a snake.

Each coordinate is a pair of numbers representing a position:

• The first number is the X position (horizontal)
• The second number is the Y position (vertical)

(2, 1)  # means X = 2, Y = 1

Let's take this example to demonstrate typical encoding

Consider this snake on a grid:

    0 1 2 3 4 5 6
  0 . . . . . . .
  1 . . H ● ● . .
  2 . . . . ● . .
  3 . . . . . . .
  4 . . . . . . .

This snake is represented as where H is the head and ● represents body segments:

[(2,1), (3,1), (4,1), (4,2)]

But how much memory does it take?

Sailing to the land of Rusty Crabs

We need to decide on the first¹ representation of this sequence in Rust.

[(2,1), (3,1), (4,1), (4,2)]

Take a top-down approach at decomposing this representation

1. It's a sequence
2. A sequence of pairs
3. A pair of x and y positions
4. x position
5. y position

From here we take a bottom-up approach:

x position and y position

• No reason for them to take differing amounts of memory
• It must be in the space of both negative and positive numbers, so we have few built-in choices:
  • isize: pointer-sized signed integer (32-bit on 32-bit systems, 64-bit on 64-bit systems)
    • Type not to be used in this context
  • i8: 8-bit signed integer (-128 to 127)
    • Likely too small
  • i16: 16-bit signed integer (-32,768 to 32,767)
    • Might suffice, but risky if requirements change
  • i32: 32-bit signed integer (-2,147,483,648 to 2,147,483,647)
    • Sweet spot
  • i64: 64-bit signed integer (-9,223,372,036,854,775,808 to 9,223,372,036,854,775,807)
    • Clearly too large

So choose i32 for both x and y positions

A pair of x and y positions

A pair is a product type² and may be represented:

• As tuple

  let as_tuple: (i32, i32) = (0, 0);
  

• As struct

  pub struct Pos {
      pub x: i32,
      pub y: i32,
  }
  

What do we choose?

• From the perspective of memory consumption:

  • Both take the same amount of memory
    • For this matter, memory layout³ for struct does not matter: #[repr(C)] or default Rust alignment take the same space

• From the perspective of usability:

  • Tuple

    let pos = (0, 0);
    let x = pos.0; // access by index in the tuple
    let y = pos.1; // access by index in the tuple
    

  • Struct

    let pos = Pos { x: 0, y: 0}
    let x = pos.x; // access by attribute name
    let y = pos.y; // access by attribute name
    

struct wins from the perspective of usability, because naming is better than indexing.

A sequence of pairs

We don't care about modifications - we care about compression of the whole state

So we won't use mutable sequences like Vec, queues, etc.

Let's pick immutable slices and be consistent to use this data structure all the way.

Example:

let positions: &[Pos] = [
    Pos { x: 0, y: 0 },
    Pos { x: 1, y: 1 },
    Pos { x: 2, y: 2 },
    Pos { x: 3, y: 3 },
]
.as_slice();

So we'll use immutable slices of sequences consisting of pairs of x and y coordinates represented as i32 composed in structs named Pos.

Memory Estimations of Current Representation

An instance of Pos size is 2 i32 sizes. So 2 * 4 bytes = 8 bytes.

The size of a sequence is proportional to the size of a snake. And after the compression it will remain true as well.

So the task is to find a more compressed view than 8 bytes * snake size.

How domain knowledge might help to optimize the memory consumption?

Well. Let's look once more at the first example.

    0 1 2 3 4 5 6
  0 . . . . . . .
  1 . . H ● ● . .
  2 . . . . ● . .
  3 . . . . . . .
  4 . . . . . . .

We see that a snake consists of connected points.

If it were to go Up it would look like:

    0 1 2 3 4 5 6
  0 . . H . . . .
  1 . . ● ● ● . .
  2 . . . . . . .
  3 . . . . . . .
  4 . . . . . . .

Interesting, so Up is a direction. Something that seems to have a place in our domain.

Let's define a sum type⁴ - an enum in Rust:

pub enum Direction {
    Up,
    Down,
    Left,
    Right,
}

Could we define a snake just in terms of directions? No.

But, if we keep the head (or tail) of the snake as a starting point, we could define the rest of the snake as a sequence of directions.

And what's interesting about Direction is that there are only 4 choices to pick from. It screams - here's our optimization.

So how many bits do we need to encode a Direction?

⌈log₂(n)⌉

where:
- n = number of possible values
- ⌈ ⌉ = ceiling function (round up to nearest integer)

So for Direction, for 4 choices: bits needed = ⌈log₂(4)⌉ = ⌈2⌉ = 2 bits.

Let's implement both encode and decode functions on Direction:

impl Direction {
    pub fn encode(&self) -> u8 {
        match self {
            Self::Up => 0b00,
            Self::Down => 0b01,
            Self::Left => 0b10,
            Self::Right => 0b11,
        }
    }

    pub fn decode(value: u8) -> Option<Self> {
        match value {
            0b00 => Some(Self::Up),
            0b01 => Some(Self::Down),
            0b10 => Some(Self::Left),
            0b11 => Some(Self::Right),
            _ => None,
        }
    }
}

We use a u8 since it's a built-in type and there isn't a u2 built-in. Since it will act as an intermediary value, it's ok.

Back to this example:

    0 1 2 3 4 5 6
  0 . . . . . . .
  1 . . H ● ● . .
  2 . . . . ● . .
  3 . . . . . . .
  4 . . . . . . .

How do we view a snake in terms of a starting point and consequent directions?

let starting_position: Pos = Pos { x: 2, y: 1 };
let consequent_directions =
    [Direction::Right, Direction::Right, Direction::Down].as_slice();

So compared to the previous representation which took 8 bytes * 4 = 32 bytes, this one takes 8 bytes + 2 bits * 3 = 8.75 bytes.

And the longer a snake - the more beneficial such optimization, since the starting point is the most expensive.

Let's define our custom packing format in terms of packing and unpacking functions

There's no good reason to pack the starting point:

• Less reusable, because a starting point can take variable size, here we chose i32
• Coupling of compressible (Direction) and uncompressible (Pos) data

This article would not exist if the next bits of code
weren't already used in my project snake

The purpose of this article is more to learn to think about problems and solve them than to use bit operations.

type DirectionsInLastByte = u8;

// packs a sequence of directions into a sequence of bytes
//
// each Direction is encoded using 2 bits because there are 4 values
// 4 directions can be encoded in 1 byte
//
// since the last partition of directions can contain 1 to 4 values,
// the serializer pads such byte with zeroes
//
// returns a pair of packed values and how many directions are in the last byte
pub fn pack_values(directions: &[Direction]) -> (Vec<u8>, DirectionsInLastByte) {
    let mut result = Vec::with_capacity((directions.len() + 3) / 4);

    for chunk in directions.chunks(4) {
        // start with empty byte
        let mut byte = 0u8;

        for dir in chunk {
            // move to left, leaving 2 bits of space
            byte <<= 2;
            // use bit OR to append 2 bit value to the end
            byte |= dir.encode();
        }

        // pad zeroes when chunk length is less than 4
        byte <<= 2 * (4 - chunk.len());

        result.push(byte);
    }

    let directions_in_last_byte = {
        let remainder = (directions.len() % 4) as u8;
        if remainder == 0 && !directions.is_empty() {
            4
        } else {
            remainder
        }
    };

    (result, directions_in_last_byte)
}

pub fn unpack_values(
    packed: &[u8],
    directions_in_last_byte: DirectionsInLastByte,
) -> Vec<Direction> {
    let mut result = Vec::with_capacity(packed.len() * 4);

    fn decode_byte(byte: u8, contains: u8) -> Vec<Direction> {
        let mut result = vec![];

        assert!(contains >= 1);
        assert!(contains <= 4);

        for i in 0..contains {
            let mask_shift = 6 - (2 * i);

            let mask = 0b11 << mask_shift;

            // extract bits using:
            // shifted 0b11 with & (removing bits to the left and right of the mask),
            // then bit shift to the right by the mask shift size,
            // leaving you with a byte not exceeding decimal value 3 (2 bits)
            let dir_encoded = (byte & mask) >> mask_shift;
            result.push(Direction::decode(dir_encoded).expect("to be packed properly"));
        }

        result
    }

    for (i, byte) in packed.into_iter().enumerate() {
        let contains = if i == packed.len() - 1 {
            directions_in_last_byte
        } else {
            4u8
        };

        result.extend(decode_byte(*byte, contains));
    }

    result
}

#[cfg(test)]
mod tests {
    use super::*;

    #[test]
    fn test_pack_unpack_values() {
        let (packed, values_in_last_byte) =
            pack_values(&[Direction::Right, Direction::Right, Direction::Down]);
        assert_eq!(packed, vec![0b11_11_01_00]);

        assert_eq!(
            unpack_values(&vec![0b11_11_01_00], values_in_last_byte),
            vec![Direction::Right, Direction::Right, Direction::Down]
        );
    }
}

Having all this we can

• Encode a snake having 2 values:

  • Starting position
  • Consequent directions

• Decode a snake having 3 values:

  • Starting position
  • What the packing function returned:
    • Packed consequent directions (where the optimization lies)
    • How many directions are in the last byte of packed directions

Our custom compression format is done

And it's battle-tested in snake

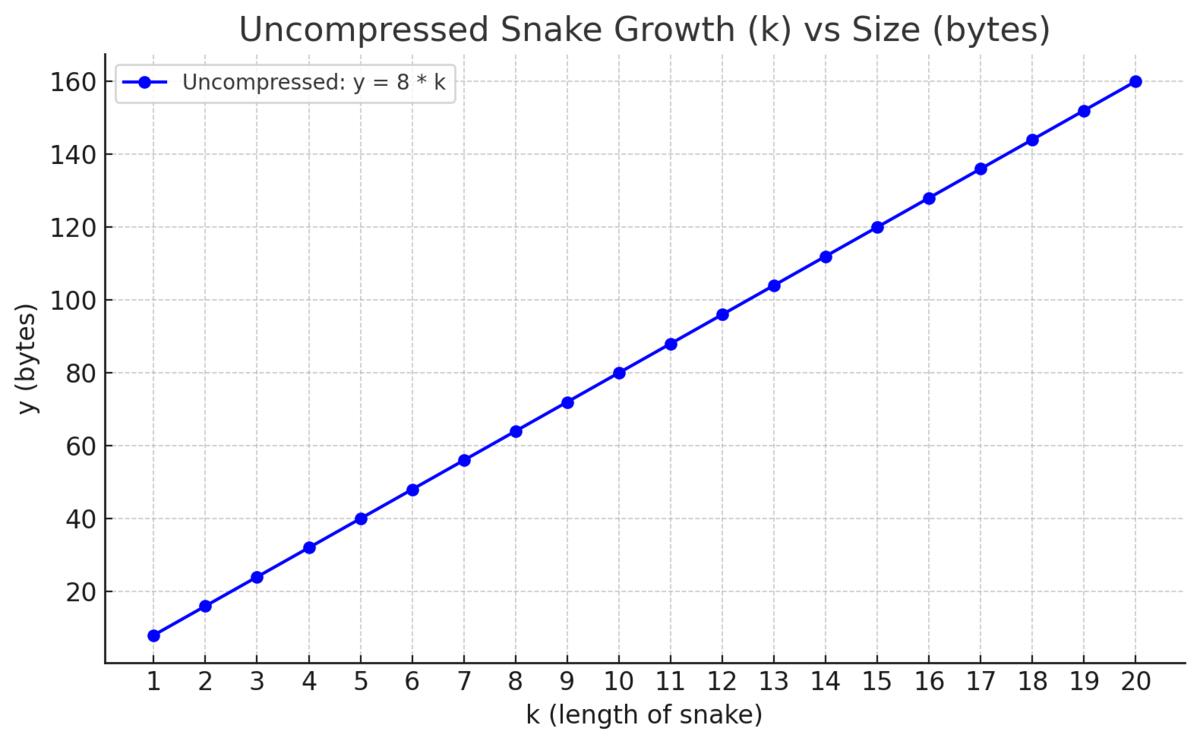
So let's plot functions depending on snake size (growth) for memory consumption with and without our custom compression

k is a length (growth) of a snake

A function without compression:

y = 8 bytes * k

A function with compression:

y = max(0, sign(k)) * 8 bytes + ceil((k - 1) / 4) bytes + 1 byte

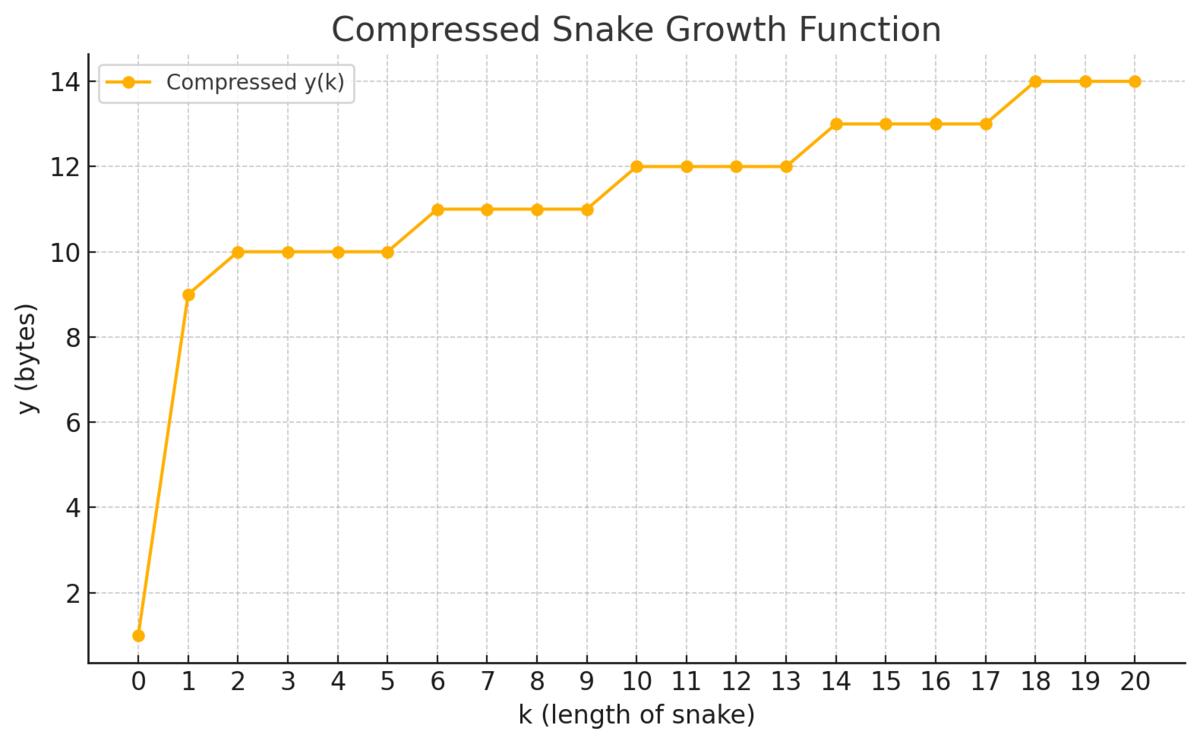
From this we can see that memory consumption with k=20 is:

• 160 bytes without compression
• 14 bytes with compression (and benefits are more significant with larger k)

Conclusion

Rarely do you solve really interesting problems (or challenge yourself this way), but coming up with your own compression algorithm is in the space of interesting problems. It brings a lot of satisfaction when it works. Especially as part of a larger process, that you can't even believe it if it works from the first try.

Supplanting to the article code repository